Structured Text Logic and Boolean Instructions | Motor Starter Interview Practice

Introduction

Structured Text handles logical and mathematical comparators similarly to other programming languages such as C, C++, Java and Python. However, their syntax may be unfamiliar to those who work on PLCs within a ladder logic environment. That being said, every branch of PLC ladder logic is a state flow that can be simplified into a logical flow thus used in a single Structured Text statement.

Mathematical comparators are also similar to what you'd expect in one of the languages mentioned above. However, the instructions one is used to in ladder logic such as LES, LIM, GRT and others are no longer available. Instead, the user is required to create logic that is similar to what one would see in a CMP Instruction. In other words, the user will have to input a mathematical instruction that would compare multiple values and return a "LOW" or "HIGH".

Working with Structured Text Logical Operators

Each logical comparator obeys simple rules which evaluate the expression and return a “0” or a “1” to the target bit based on the status of other bits. We’ll start with a simple example and work our way to a complex problem.

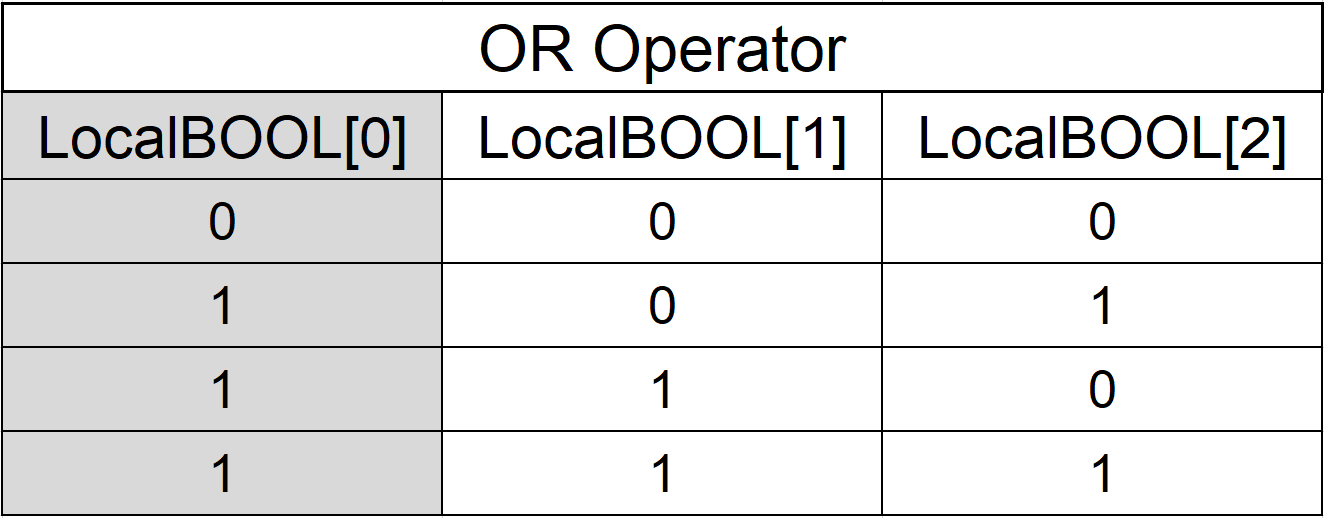
OR Operator

The OR operator will evaluate to “1” if either of the tags are set to “1”.

Example of Expression

LocalBOOL[0] := LocalBOOL[1] OR LocalBOOL[2];

Truth Table

Ladder Logic Equivalent

The equivalent in ladder logic of the OR operator is a branch statement. In other words, the same exact outcome would occur within a rung structured as the one shown below.

AND Operator

The AND operator will evaluate to “1” if both of the tags are set to “1”.

Example of Expression

LocalBOOL[0] := LocalBOOL[1] AND LocalBOOL[2];

Truth Table‍

Ladder Logic Equivalent

The equivalent in ladder logic of the AND operator is a sequential XIC statement that evaluates and OTE Instruction.

NOT Operator

The NOT operator will evaluate to “1” if the tag is "0" and to "0" if the tag is set to "1".

Example of Expression

LocalBOOL[0] := NOT(LocalBOOL[1]);

Truth Table‍

Ladder Logic Equivalent

The equivalent in ladder logic of the NOT operator is an XIO Instruction paired with an OTE. The goal here is to reverse the status of the bit.

‍

Structured Text Multi-Operator Expressions

Just as we can structure any combination of XIC and XIO instructions in ladder logic, we can create intricate sequences in Structured Text. Let's look at a few examples, understand how they evaluate and consider the ladder logic counterparts of the same outcome.

Motor Starter Example

The basic motor starter circuit often comes up in interviews. It's the easiest way to gauge basic PLC knowledge and see how a candidate adapts to the challenge, expands on it and discusses ways to use it in an application. Below is a simple implementation in ladder logic.

Truth Table

Based on the table presented above, we can figure out the appropriate structure for the Structured Text expression or we can convert the ladder logic we've looked at previously. As you go through these exercises a number of times, the conversion won't have to take place. Instead, you'll think of the logical operators you need to make the program execute as you intend.

The first branch of the circuit can be replaced by an OR statement while the XIO of the Stop Push Button is translated to an AND and NOT instruction.

Structured Text Equivalent

MTR1[2] [:=] ( MTR1[0] OR MTR1[2] ) AND NOT(MTR1[1]);

Complex Ladder Logic Example

Here's an example you can analyze for practice. If you're able to convert the following rung to a structured text statement you've grasped the above concepts well.

We can approach the example above in a steps to simplify our task.

Step 1 - We've learned that each sequential array of tags is equivalent to an AND statement. Also, we know that an XIO requires a NOT.

Branch 1 - BOOL[1] AND BOOL[2] AND NOT(BOOL[3])

Branch 2 - BOOL[4] AND BOOL[5]

Branch 3 - NOT(BOOL[6])

Step 2 - We note that branch 3 is paired with the BOOL[4] tag only! We can combine Branch 2 and 3 like so.

Branch 2 & 3 - (BOOL[4] OR NOT(BOOL[6])) AND BOOL[5]

Step 3 - We combine everything.

Final Logic - (BOOL[1] AND BOOL[2] AND NOT(BOOL[3])) OR ((BOOL[4] OR NOT(BOOL[6])) AND BOOL[5])

Structured Text Expression

BOOL[7] [:=] (BOOL[1] AND BOOL[2] AND NOT(BOOL[3])) OR ((BOOL[4] OR NOT(BOOL[6])) AND BOOL[5])

Working with Boolean Operators

In ladder logic, we have access to multiple mathematical expressions and operators that allow us to easily evaluate expressions. Instructions such as GRT, LES, LIM, NEQ, and more are commonplace in ladder logic programs. However, these instructions aren't available in Structured Text. How can we evaluate such comparisons? The answer is through an expression equivalent to what one would use in a CMP Instruction.

It's much easier to learn by example, so let's see a few expressions in structured text and discuss what they evaluate to.

BOOL[1] := DINT[0] > 100; - Is equivalent to a GRT instruction that will set a BOOL[1] OTE once the value stored in the DINT[0] register exceeds 100.

BOOL[1] := DINT[0] + 10 < 567; - Is the equivalent of a LES expression that evaluates to true when DINT[0] + 10 is less than 567.

You may only use a single operator within a structured text expression. Therefore, in order to achieve the effect of a LIM instruction we had in ladder logic, you'll have to evaluate the expressions separately and then combine them through logic.

Conclusion

Working with structured text operators is similar to what you would see in other programming languages. However, the transition may seem challenging when the user was only exposed to ladder logic. With the examples we've covered in our tutorial, the transition should be much simpler. It's important to memorize the different operators you're used to implement through ladder logic rung structures.

The mathematical comparators aren't available in structured text programming. The users are required to use expressions that evaluate to a "HIGH" or "LOW" based on a condition. Through the use of such expressions, programmers can achieve any of the outcomes of the mathematical instructions available in ladder logic.